centro de gravedad

 

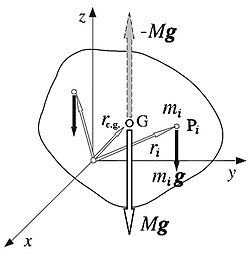
El centro de gravedad es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas porciones materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo.


En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo.

El c.g. de un cuerpo no corresponde necesariamente a un punto material del cuerpo. Así, el c.g. de una esfera hueca está situado en el centro de la esfera que, obviamente, no pertenece al cuerpo

Diapositivas de ayuda centroides_y_CDG.pptx (848235)

Cálculo del centro de gravedad

 

 
Centro de gravedad.

El centro de gravedad de un cuerpo viene dado por el único vector que cumple que:

\mathbf r_\text{c.g.}\times M\mathbf{g}(\mathbf{r}_\text{c.g.}) = \int_V \mathbf r \times \mathbf{g}(\mathbf{r})\rho(\mathbf{r})dV

  • En un campo gravitatorio uniforme, es decir, uno en que el vector de campo gravitatorio \mathbf{g} es el mismo en todos los puntos, la definición anterior se reduce a la definición del centro de masas:

\mathbf{r}_\text{c.m.} = \frac{1}{M}\int_V \mathbf{r} \, \rho(\mathbf{r})dV

  • En el campo gravitatorio creado por un cuerpo material cuya distancia al objeto considerado sea muy grande comparado con las dimensiones del cuerpo y del propio objeto, el centro de gravedad del objeto viene dado por:

\frac{\hat{\mathbf{u}}_\text{c.g.}}{r_\text{c.g.}^2} = \int_V \frac{\hat{\mathbf{u}}_r}{r^2}\ dV

Ejemplo. Dada una barra homogénea de longitud L, orientada hacia un planeta lejano, y cuyo centro de masa dista una distancia Dc.m.,del centro del planeta, el centro de gravedad de la barra está situado a una distancia del centro del planeta dado por:
D_\text{c.g.} = \sqrt{D_\text{c.m.}^2-\frac{L^2}{4}} \approx D_\text{c.m.}\left(1-\frac{L^2}{8D_\text{c.m.}^2} \right)
La diferencia entre centro de masas y el centro de gravedad se debe en este caso a que el extremo de la barra más cercano al planeta es atraído gravitatoriamente con mayor intensidad que el extremo más alejado.

 

RESISTENCIA DE MATERIALES

ESTRUCTURAS
y
CONSTRUCCIÓN

En el curso de MECÁNICA se empezaron a estudiar los elementos estructurales y las estructuras desde el punto de vista del EQUILIBRIO ESTÁTICO externo, es decir de la QUIETUD en que deben estar para que cumplan su función. Se tenían por ejemplo las siguientes situaciones y se hacía un

DIAGRAMA DE CUERPO LIBRE en el cual se ponían todas las fuerzas externas que actuaban sobre el mismo y a continuación se aplicaban las ecuaciones de equilibrio con el fin de encontrar las reacciones en los apoyos.

En los casos mostrados en la figura, las reacciones se calculan mediante la aplicación de las ecuaciones de equilibrio (suma de fuerzas igual a cero y suma de momentos igual a cero). Aunque el cálculo de las reacciones que garanticen el reposo es fundamental, éste es solo el primer paso en el proceso de análisis y diseño que en cada situación llevará a la definición del tipo de material, de la forma y de las dimensiones que harán que las estructuras sean seguras y funcionales.

- Seguras quiere decir que no se rompan.

- Funcionales quiere decir que no se deformen excesivamente afectando el servicio que prestan.

Estas dos condiciones, RESISTENCIA y RIGIDEZ deberán asegurarse para que las estructuras cumplan su fin.

Es claro que en las situaciones mostradas a continuación las estructuras pueden romperse o deformarse excesivamente.

Como puede verse, cualquiera de las dos situaciones (Deformación excesiva o Rotura) es inadmisible.

Por lo tanto, el ingeniero debe asegurar con una buena probabilidad de éxito que las estructuras que construya sean RÍGIDAS y RESISTENTES.

De esto trata la RESISTENCIA DE MATERIALES. Debemos ser capaces de garantizar que las estructuras a construir no se deformen excesivamente y que no se fracturen.

Para hacerlo, es necesario que sepamos calcular las fuerzas internas que se producen en los elementos estructurales y que son en últimas las que producirán las deformaciones y la rotura.

En general podemos afirmar que una fuerza interna produce un esfuerzo actuante que trata de romper el elemento. Que se rompa depende del esfuerzo resistente que tenga el elemento el cual  dependerá del material y de sus dimensiones transversales.

Análogamente, esas mismas fuerzas internas producirán deformaciones del elemento las cuales dependerán igualmente del material y de sus dimensiones.

La Resistencia de Materiales se ocupa del cálculo de los esfuerzos y deformaciones que se producirán debiendo garantizar el ingeniero que las deformaciones estén dentro de unos límites permisibles y obviamente que no se produzcan roturas.

Los esfuerzos resistentes del material deben calcularse con el fin de poder compararlos con los  esfuerzos actuantes. Estos esfuerzos dependen no solo de las dimensiones del elemento estructural  sino de la forma como estén aplicadas las cargas las cuales pueden producir esfuerzos normales o

cortantes dependiendo de que las fuerzas o momentos actuantes sean axiales, transversales o combinados.

Debe por tanto determinarse primero que todo si el elemento en estudio está sometido a fuerzas axiales, transversales (en cuyo caso se producirá flexión), momentos torsionales (torsión) o una combinación de algunos de ellos.

Equilibrio y elasticidad Condiciones de equilibrio

Una partícula esta en equilibrio si la resultante de todas las fuerzas (externas) que actúan 
sobre ella es cero
· Para cuerpos con extensión finita: 

 

el centro de masa del cuerpo debe haber una aceleración cero

Una ayuda en problemas resueltos

equilibrio-estatico-elasticidad.pdf (345353)

MECANICA DE FLUIDOS 

La materia puede clasificarse por su forma física 
como un sólido, un líquido o un gas. Las moléculas 
de los s6lidos a temperaturas y presiones ordinarias 
tienen atracción fuerte entre ellas y permanecen en 
posición fija relativa una a la otra. Luego un sólido 
tiene volumen y forma definida y sufre 
deformaciones finitas bajo la acción de una fuerza. 
Las moléculas de los líquidos a temperaturas y 
presiones ordinarias tienen poca atracción entre ellas 
y cambian de posición relativa una a otra. En 
consecuencia los líquidos tienen volumen definido 
tomando la forma del recipiente que los contiene, 
pero no lo llenan necesariamente. 
Las moléculas de los gases a. temperaturas y 
presiones ordinarias tienen muy poca atracción entre 
ellas y tienen un movimiento al azar, o sea que los 
gases no tienen volumen ni forma definidas, adoptan 
la forma del recipiente que los contiene y lo llenan 
completamente. : . 
A causa de que los líquidos y gases a temperaturas y 
presiones ordinarias no resisten la acción de un 
esfuerzo cortante y continúan deformándose bajo su 
acción, son conocidos como fluidos. 
La rama de la Física que estudia los efectos de las 
fuerzas que actúan sobre 1os fluidos se denomina 
Mecánica de Fluidos, tradicionalmente subdividida 
en dos partes estática y dinámica. 
Estática de los fluidos, estudia el equilibrio de los 
fluidos bajo la acción de fuerzas estacionarias. 
Dinámica de los fluidos, estudia el movimiento de 
los fluidos y las causas que la producen, sostienen o 
se oponen a este movimiento.
 
 Ecuaciones Generales de la Mecanica de Fluidos
 

-Forma integral: \frac{d}{dt}\int_{\Omega} \rho \; d\Omega = -\int_{\partial\Omega} \rho (\mathbf{v\cdot n})\ d(\partial\Omega)

-Forma diferencial: \frac{\partial \rho}{\partial t} + \nabla\cdot\left(\rho\mathbf{v}\right) = 0

Ecuación de cantidad de movimiento:

-Forma integral: \frac{d}{dt}\int_{\Omega} \rho\mathbf{v} \; d\Omega +\int_{\partial\Omega} \rho\mathbf{v}(\mathbf{v\cdot n})\ d\partial\Omega= \int_{\partial\Omega} \boldsymbol\tau \mathbf{\cdot n}\ d\partial\Omega+ \int_{\Omega} \rho\mathbf{f} d\Omega

-Forma diferencial: \frac{\part}{\part t}\left(\rho \mathbf{v} \right) + \nabla \cdot (\rho \mathbf{v} \otimes \mathbf{v}) = \rho \mathbf{f}+\nabla \cdot \boldsymbol\tau.

Ecuación de la energía

-Forma integral: \frac{d}{dt}\int_{\Omega} \rho\left (e+\frac {1}{2}v^2\right)\; d\Omega+\int_{\partial\Omega} \rho\left (e+\frac {1}{2}v^2\right)\mathbf{v\cdot n} d\partial\Omega=\int_{\partial\Omega} \mathbf{n}\cdot\tau\cdot\mathbf{v} \; d\partial\Omega+\int_{\Omega} \rho\mathbf{f\cdot v} \;d\Omega-\int_{\partial\Omega} \mathbf {q \cdot n} \; d\partial\Omega

-Forma diferencial: \rho\frac {D}{Dt}\left(e+\frac {1}{2}v^2 \right )=-\nabla\cdot\left(p\mathbf{v}\right)+\nabla\cdot\left(\tau'\cdot\mathbf{v}\right)+ \rho\mathbf{f\cdot v}+\nabla\cdot\left(k\nabla T\right)

 
 Ejerccios Propuestos Mecanica Fluida
 

 

LOS GASES

Leyes de los gases

LEY DE CHARLES 

La ley de Charles, o ley de los volúmenes, fue descubierta en 1778. Se dice que, para un gas ideal a presión constante, el volumen es directamente proporcional a la temperatura absoluta (en grados Kelvin).

Esto se puede encontrar utilizando la teoría cinética de los gases o un recipiente con calentamiento o enfriamiento [sin congelar <0] con un volumen variable (por ejemplo, un frasco cónico con un globo).

V = k_2T \,

Donde T es la temperatura absoluta del gas (en grados Kelvin) y k2 (en m3·K−1) es la constante producida.

Ley de Gay-Lussac

Postula que si se mantiene constante el volumen de un gas y se aumenta su temperatura, la presión del mismo aumenta proporcionalmente

 

Condiciones normales

Se denominan condiciones normales (C.N.) a las siguientes condiciones de presión y temperatura:
 
P = 1 atmósfera
T = 0 ºC = 273 K
 

LAS LEYES DE LOS GASES IDEALES

Combinación de las leyes de los gases:

 

Ecuación de los gases ideales.

  1. Ley de Boyle  V µ 1/P
  2. Ley de Charles     V µ T
  3. Ley de Avogadro V µ n

            PV = nRT

Ejerccios Propuestos 

En esta pagina encontraremos ejerccios resueltos sobre el tema , que nos facilitaran a saber del tema

https://www.fisicanet.com.ar/fisica/gases/tp01_gases_ideales.php

CALOR

CAMBIO DE ESTADO DE LA MATERIA

 

En física y química se denomina cambio de estado la evolución de la materia entre varios estados de agregación sin que ocurra un cambio en su composición. Los tres estados más estudiados y comunes en la Tierra son el sólido, el líquido y el gaseoso; no obstante, el estado de agregación más común en el Universo es el plasma, material del que están compuestas las estrellas (si se descarta la materia oscura).

 

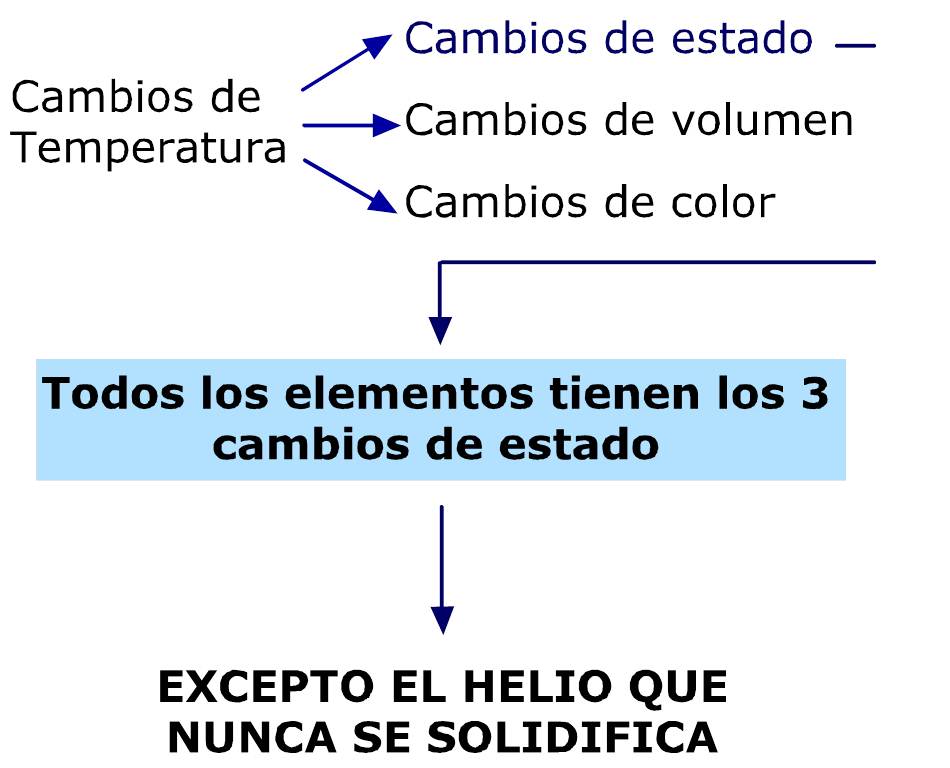
Cambios de estado de agregación de la materia

Son los procesos en los que un estado de la materia cambia a otro manteniendo una semejanza en su composición. A continuación se describen los diferentes cambios de estado o transformaciones de fase de la materia:
Fusión: Es el paso de un sólido al estado líquido por medio del calor; durante este proceso endotermico (proceso que absorbe energía para llevarse a cabo este cambio) hay un punto en que la temperatura permanece constante. El "punto de fusión" es la temperatura a la cual el sólido se funde, por lo que su valor es particular para cada sustancia. Cuando dichas moléculas se moverán en una forma independiente, transformándose en un líquido.
Solidificación: Es el paso de un líquido a sólido por medio del enfriamiento; el proceso es exotérmico. El "punto de solidificación" o de congelación es la temperatura a la cual el líquido se solidifica y permanece constante durante el cambio, y coincide con el punto de fusión si se realiza de forma lenta (reversible); su valor es también específico.
Vaporización y ebullición: Son los procesos físicos en los que un líquido pasa a estado gaseoso. Si se realiza cuando la temperatura de la totalidad del líquido iguala al punto de ebullición del líquido a esa presión continuar calentándose el líquido, éste absorbe el calor, pero sin aumentar la temperatura: el calor se emplea en la conversión del agua en estado líquido en agua en estado gaseoso, hasta que la totalidad de la masa pasa al estado gaseoso. En ese momento es posible aumentar la temperatura del gas.
Condensación: Se denomina condensación al cambio de estado de la materia que se pasa de forma gaseosa a forma líquida. Es el proceso inverso a la vaporación. Si se produce un paso de estado gaseoso a estado sólido de manera directa, el proceso es llamado sublimación inversa. Si se produce un paso del estado líquido a sólido se denomina solidificación.
Sublimación: Es el proceso que consiste en el cambio de estado de la materia sólida al estado gaseoso sin pasar por el estado líquido. Al proceso inverso se le denomina Sublimación inversa; es decir, el paso directo del estado gaseoso al estado sólido. Un ejemplo clásico de sustancia capaz de sublimarse es el hielo seco.

Calor y primera ley de la termodinámica

Energía interna

La energía interna es toda la energía que pertenece a un sistema mientras está estacionario (es decir, no se traslada ni rota), incluida la energía nuclear, la energía química y la energía de deformación (como un resorte comprimido o estirado), así como energía térmica. 

Energía Térmica

La energía térmica es la parte de la energía interna que cambia cuando cambia la temperatura del sistema.

El término calor se utiliza para dar entender tanto energía térmica como transmisión de energía térmica.

Cuando cambia la temperatura de un sistema y en el proceso cambia la temperatura de un sistema vecino, decimos que ha habido flujo de calor que entra o sale del sistema.

Unidades de calor

La caloría fue definida como la cantidad de calor necesaria para elevar la temperatura de 1 g de agua de 14.5ºC a 15.5ºC.

La unidad de calor en el sistema ingles es la unidad térmica británica (Btu), definida como el calor necesario para elevar la temperatura de 1 lb de agua de 63ºF a 64ºF.

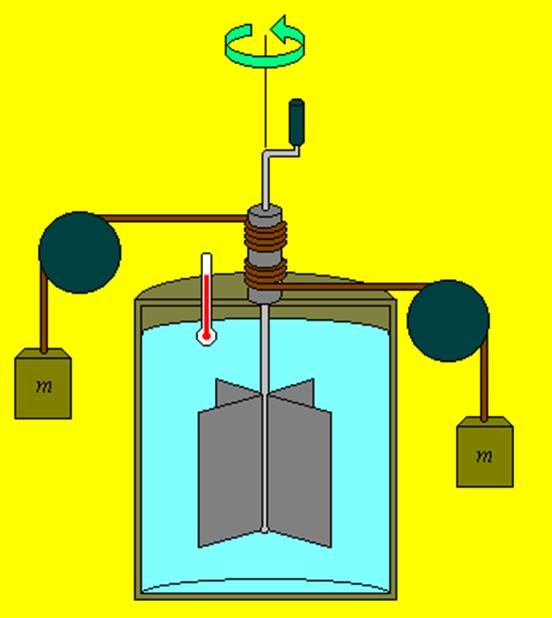
El equivalente mecánico del calor

4.1858 J de energía mecánica elevaban la temperatura de 1 g de agua de 14.5ºC a 15.5ºC.

Éste valor se conoce como el equivalente mecánico del calor. 

Ejemplo :

La energía requerida para aumentar la temperatura de 0.50 kg de agua en 3°C es:

  Q = mcDT = (0.5)(4186)(3) = 6.28 x 103 J.

Donde c = 4186 J/kg °C

Calor latente

Los cambios de sólido a líquido, de líquido a gas y los opuestos, se llaman cambios de fase.

La energía térmica necesaria para cambiar de fase una masa m de una sustancia pura es

  Q = mL

Donde L es el calor latente (calor oculto) de la sustancia.

Existen dos tipos de calor latente:

Lf – calor latente de fusión

Lv – calor latente de vaporización

Ejemplo :

¿Qué masa de vapor inicialmente a 130°C se necesita para calentar 200 g de agua en un recipiente de vidrio de 100 g de 20.0 a 50.0 °C?

Para enfriar el vapor

Q1 = mcDT = m(2010)30 = 60300m J

Para condensar el vapor se libera:

Q2 = mLf = m(2.26x106)

Para calentar el agua y el recipiente se requiere:

Q3 = mwcwDT + mVcvDT = (0.2)(4186)(30) + (0.1)(837)(30) = 27627

Para enfriar el vapor (agua) de 100°C a 50°C

Q3 = mcwDT = m(4186)(50) = 209300

Calor perdido por el vapor = Calor ganado por agua y recipiente

60300m + 2260000m + 209300m = 27627

m = 10.9 g

Ejerrcios Propuestos :

https://www.fisica-facil.com/Temario/Termodinamica/Ejercicios/Calor%20y%20temperatura/temario.htm

 

 

Distribución de la Energía
ENTROPIA

1. Dirección de los procesos termodinámicos

  1. Los procesos en la naturaleza son irreversibles. 
  2. Todo sistema tiende a un estado menos ordenado.
  3. Procesos idealizados

2. Entropía

  1. Es una medida cuantitativa del desorden
  2. Se define el cambio infinitesimal de entropía dS durante un proceso reversible como

Expansión libre

  • Supongamos el gas recluido en un recipiente aislado de su entorno. Sobre él no se realiza ningún trabajo.
  • DU=0,  W=0, Q=0
  • El gas se encuentra en un volumen V1. Al abrir la compuerta se expandirá hasta ocupar todo el volumen.
  • Es un proceso irreversible.
  • Para calcular la variación de entropía debemos imaginar un proceso reversible que conecte los dos estados.

 

Otras Formulaciones

Máquina térmica (Kelvin):

Es imposible extraer calor de un sistema a una sola temperatura y convertirlo en trabajo mecánico sin que el sistema o los alrededores cambien de algún modo.

Refrigerador térmico (Clausius):

 Es imposible un proceso espontáneo cuyo único resultado sea el paso de calor de un objeto a otro de mayor temperatura.

Máquinas térmicas y la segunda ley de la termodinámica

La segunda ley de la termodinámica establece cuáles procesos pueden ocurrir y cuáles no en la naturaleza. Los siguientes son ejemplos de procesos que son consistentes con la primera ley de la termodinámica pero que proceden de un orden gobernado por la segunda ley:

Cuando dos objetos a diferente temperatura se ponen en contacto térmico entre sí, la energía térmica siempre fluye del objeto más caliente al más frío, nunca del más frío al más caliente.

Una bola de hule que se deja caer al suelo rebota varias veces y finalmente queda en reposo, pero una bola que se encuentra en el suelo nunca empieza a botar por sí sola.

 

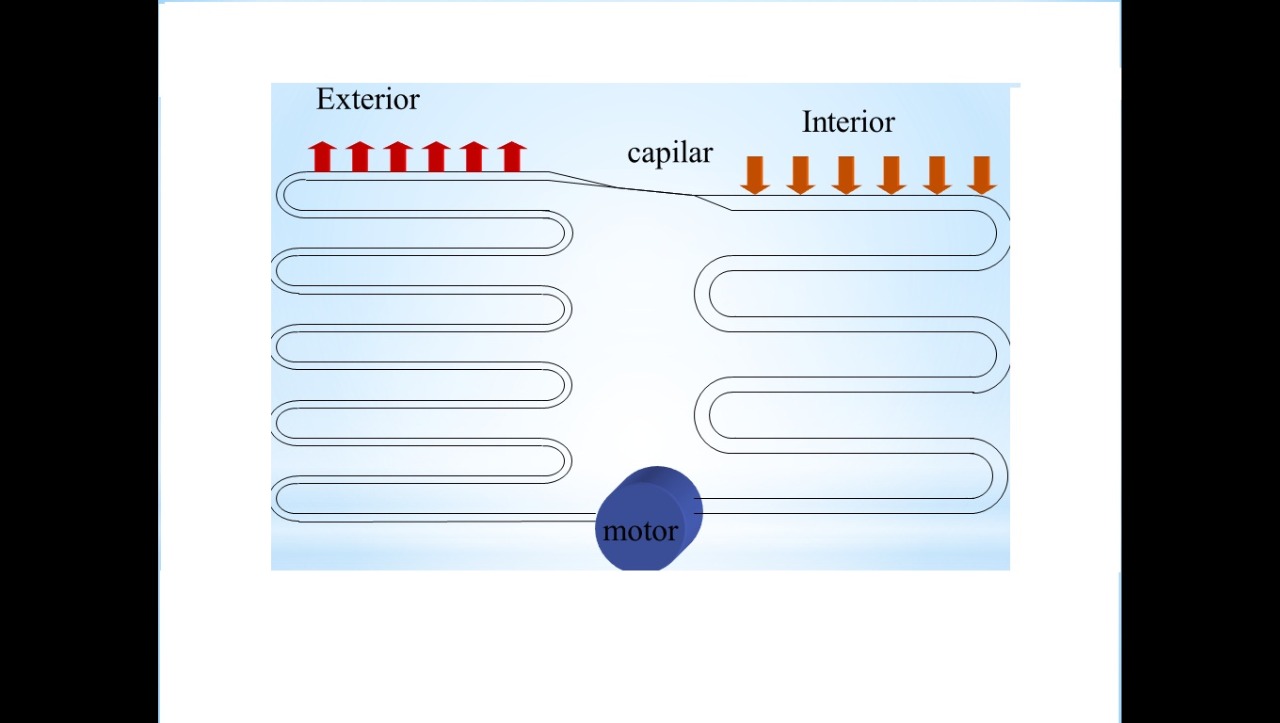
Calcule la eficiencia de una máquina térmica que absorbe 2000 J de energía de un depósito caliente y entrega 1500 J a un depósito frío.

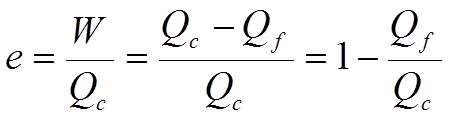
Refrigeradores y bombas de calor

Los refrigeradores y las bombas de calor son máquinas térmicas que operan a la inversa. La máquina absorbe energía térmica Qf del depósito frío y entrega energía térmica Qc al depósito caliente.

 

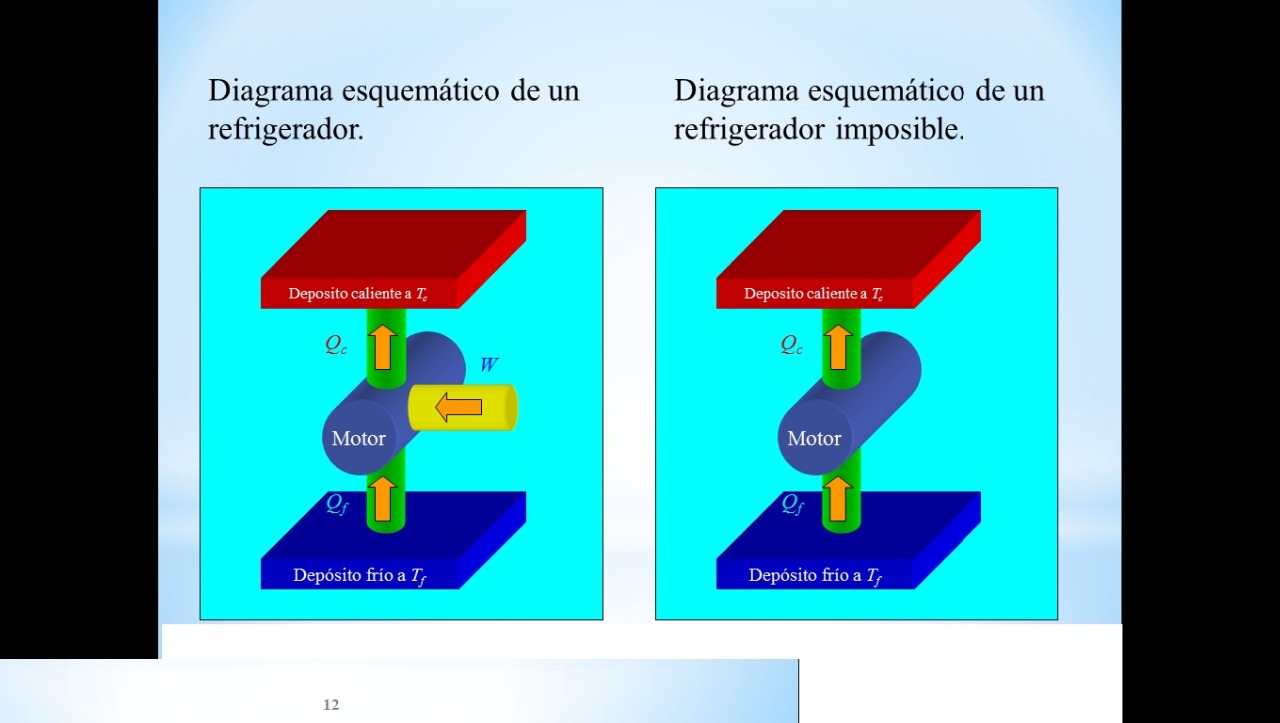
Funcionamiento

Todo liquido que se evapore fácilmente a bajas temperaturas es un potencial refrigerante.

Es posible evaporarlo y licuarlo alternadamente, haciéndolo circular a través de tubos en los que varíe la presión.

En la mayoría de los refrigeradores domésticos, el refrigerante es uno de los compuestos conocidos como clorofluorocarbonos o freones.

Los tubos del interior del refrigerador son de grueso calibre, por lo que dentro de ellos la presión es baja y el líquido que allí circula se evapora. Con ello se mantiene frió el tubo y se absorbe el calor de los alimentos.

Ejemplo :

Cierto refrigerador tiene un CDR de 5. Cuando el refrigerador está en funcionamiento, su potencia de entrada es de 500 W. Una muestra de agua de 500 g de masa a 20ºC de temperatura se coloca en el compartimiento del congelador. ¿Cuánto tarda en congelar el agua a 0º C? suponga que las otras partes del refrigerador permanecen a la misma temperatura y no hay fugas de energía al exterior, así que la operación del refrigerador resulta en sólo la energía que se extrae del agua.

 

Calor extraído del agua:  Qf = mcDT – mLf = m (cDT – Lf )

Energía proporcionada al refrigerador: CDR = Qf / W

W = Qf /  CDR

Potencia: P = W/Dt   Dt = W/P

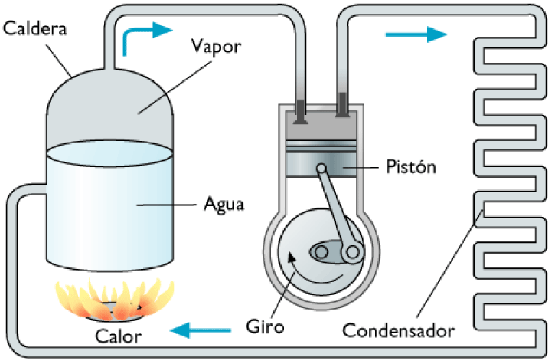
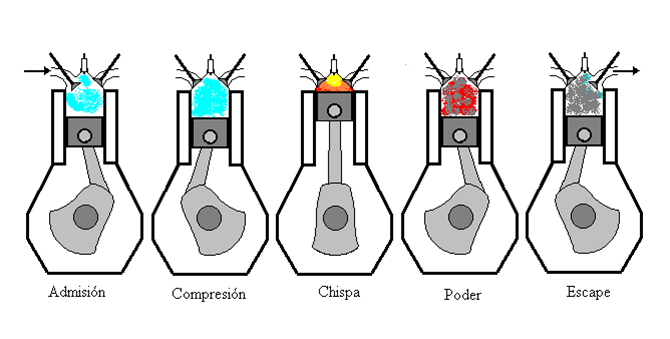
El motor de gasolina

El motor de gasolinas puede describirse mediante el ciclo Otto, el cual se ilustra en la figura

 

Cambio de entropía en un proceso de fusión

Un sólido tiene un calor latente de fusión Lf se funde a una temperatura Tm. Calcule el cambio en la entropía

 

Un cubo de hielo se funde, 3 cm de lado, 30 cm3 de volumen, L = 3.33x105 J/kg.

DS = (0.030 kg)(3.33x105 J/kg)/(273 K) = 40 J/K